Research
Piano Music Transcription
Automatic Music Transcription (AMT) is the process of inferring a symbolic music representation (e.g., a music score, a MIDI piano-roll) from music audio. It is one of the most fundamental problems in computer audition and music information retrieval, with broad applications in music source separation, content-based music retrieval, music performance analysis, and music education. We propose a novel AMT approach for piano performances. Compared to existing approaches, it has the following advantages:
- Note-level transcription: most existing AMT methods first estimate pitches in each individual time frame, and then form notes in a post-processing stage. This approach usually ignores the temporal evolution of notes, which is significant in piano music as different partials decay at different rates. Our approach transcribe notes directly from the audio waveform and it models the temporal evolution of notes.
- Time-domain transcription: Most existing AMT algorithms operate in the frequency domain through time-frequency analysis such as the short-time Fourier transform (STFT) or its variants. This introduces the well-known time/frequency resolution trade-off, also called the Gabor Limit. Our approach transcribes music in the time domain, and avoids this tradeoff.
- High transcription accuracy: Our approach outperforms a current state-of-the-art AMT method by over 20% in median F-measure, achieving a median F-measure of over 80% on acoustic piano, and drastically increases both time and frequency resolutions, especially for the lowest octaves of the piano keyboard.
- High onset detection precision: Our approach achieves a much higher time precision (~5 ms) of piano note onset detection than existing approaches (~50 ms).
- Works in reverberant environments: Most existing methods are designed and tested only in anechoic environments. Our approach works in reverberant environments, if it is trained in the same environment.
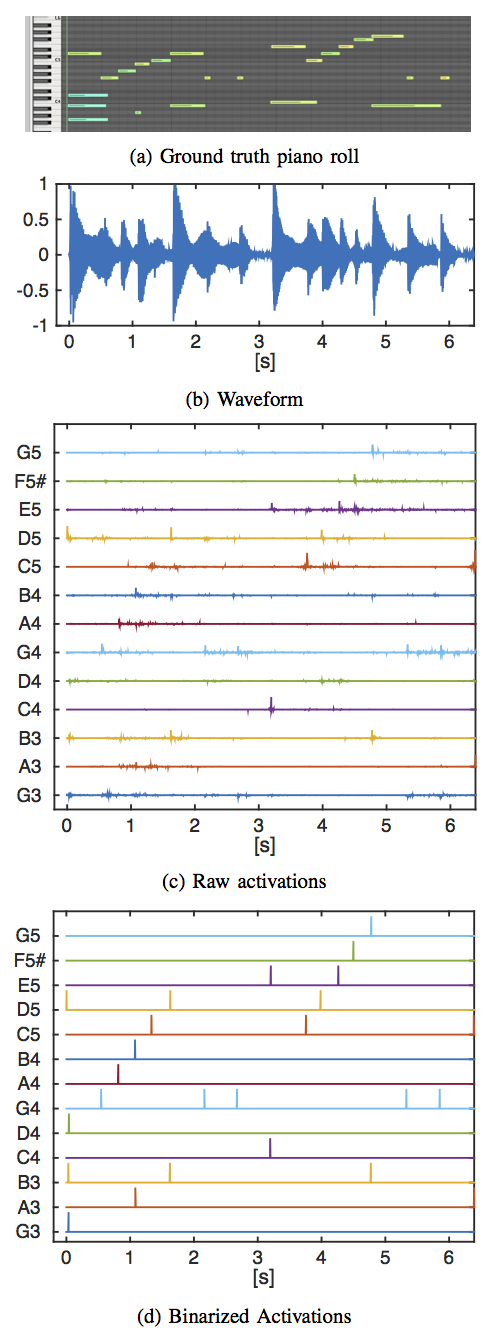
Approach: We model the piano music audio as a convolution of note waveform templates with their activations, and use an efficient convolutional sparse coding algorithm for transcription. With pre-record waveform templates of each piano key (dictionary), the algorithm is able to efficiently estimate their activations (i.e., note onsets). The picture on the left shows the basic steps of the proposed method. After the training period, which consists of recording each individual note of a piano played for 1 s at roughly the same dynamic level, preferably forte, we can transcribe an audio signal, here represented as the waveform in (b). The convolutional sparse coding algorithm estimates the activations of the dictionary elements in the audio mixture, resulting in noisy raw activations vectors as in (c). Sparse peak picking and thresholding are used to obtain the binarized activations in (d), in which each impulse corresponds to the activation of the corresponding pitch. The ground truth of the musical excerpt is shown in (a).
Condition: our approach works in a context-specific scenario, i.e., the dictionary is trained and tested on the same piano and in the same recording environment. This restricts our approach from generalizing the dictionary trained for one piano/environment to another. However, the training process is very simple, and the high accuracy and time precision of the transcription still makes our approach useful in many scenarios. Imagine that one wants to transcribe a famous Jazz pianist’s concert. Setting up the stage would take at least 1 hour. Now with an additional 5-minute training phase, the system can transcribe the pianist’s improvisations very accurately through the concert.
Demos
Here you can play a few examples of the transcriptions that can be obtained with the proposed method. The transcriptions have been rendered with a virtual piano. The initial algorithm could only estimante the note onsets but not the length of the notes. Current research is focused on overcoming this limitation, a couple of examples are provided as well.
| Description | Original Audio | Transcription |
|---|---|---|
| Bach's Minuet in G transcribed with onset detection only | Original | Transcription |
| Chopin's Etude Op. 10 No. 1 transcribed with onset detection only | Original | Transcription |
| Chopin's Etude Op. 10 No. 1 with artificial reverb (T60 = 2.5 s) | Original | Transcription |
| Bach's Minuet in G transcribed with note length estimation | Original | Transcription |
| Chopin's Etude Op. 10 No. 1 transcribed with note length estimation | Original | Transcription |